El caudalímetro de vórtice es un caudalímetro volumétrico que se investiga y produce según el principio de vórtice de Karman para medir el caudal volumétrico de gas, vapor o líquido, el caudal volumétrico de la condición estándar o el caudal másico.
Se utiliza principalmente para la medición de caudal de fluidos medios de tuberías industriales, como gas, líquido, vapor y otros medios.
Se caracteriza por una pequeña pérdida de presión, un amplio rango de medición y una gran precisión.
Apenas se ve afectado por la densidad del fluido, la presión, la temperatura, la viscosidad y otros parámetros al medir el caudal volumétrico en condiciones de trabajo.
No hay piezas mecánicas móviles, por lo que la fiabilidad es alta y el mantenimiento es reducido. Los parámetros del instrumento pueden ser estables durante mucho tiempo. El medidor de flujo de vórtice adopta un sensor de tensión piezoeléctrico, que tiene una alta fiabilidad y puede trabajar en el rango de temperatura de trabajo de -20℃~+250℃. Tiene una señal estándar analógica y una salida de señal de pulso digital.
Es fácil de utilizar con sistemas digitales como los ordenadores. Es un instrumento de medición relativamente avanzado e ideal.
Los caudalímetros de vórtice miden la velocidad del fluido utilizando un principio de funcionamiento denominado efecto von Kármán, según el cual, cuando el flujo pasa por un cuerpo de vórtice, se genera un patrón repetitivo de vórtices arremolinados.
El caudalímetro de vórtice utiliza el principio de oscilación del fluido para medir el caudal. Cuando el fluido atraviesa el caudalímetro de vórtice en la tubería, se generan alternativamente dos filas de vórtices proporcionales a la velocidad del caudal hacia arriba y hacia abajo tras el generador de vórtices de la columna triangular. La frecuencia de liberación del vórtice es proporcional a la velocidad del caudal. La velocidad media del fluido que fluye a través del generador de vórtices está relacionada con la anchura característica del generador de vórtices, y puede expresarse mediante la siguiente fórmula:
donde: f es la frecuencia de liberación del vórtice, unidad en Hz; v es la velocidad media del fluido que fluye a través del generador de vórtice, unidad en m/s, d es la anchura característica del generador de vórtice, la unidad es m; St es el número de Strouhal, adimensional, y su rango numérico es 0,14-0,27.
St es función del número de Reynolds
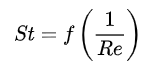
Cuando el número de Reynolds Re está dentro del intervalo, el valor de St es aproximadamente 0,2. En la medición, tratar de satisfacer el número de Reynolds del fluido en
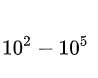
y la frecuencia del vórtice en este momento es
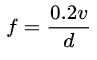
Así, midiendo la frecuencia del vórtice, se puede calcular la velocidad media “v “del fluido que fluye a través del generador de vórtice, q=vA, y luego se puede calcular el caudal “q” a partir de la fórmula, donde “A “es el área de la sección transversal del fluido que fluye a través del generador de vórtice
